El arte y la ciencia aligeran las mismas proporciones sutiles en las ramas de los árboles

¿Los artistas y científicos ven lo mismo en forma de tronco? Como científico que estudia la delimitación en los seres vivos, empiezo a pensar que sí.

‘Tableau y’ Pintor Piet Mondrian, 1921. Museo de arte The Hague

Piet Mondrian fue un resumen de la edad temprana de los artistas y el arte del arte obsesionado con la simplicidad y la esencia de la forma. Incluso las personas que nunca han oído hablar de Mondrian probablemente reconocerán su red irregular del rectángulo.

Cuando vi la “madera gris” de 1911 de Mondrian, inmediatamente reconocí algo sobre los árboles que luché para describir. Al eliminar todo, pero los elementos más importantes en la imagen abstracta, Mondrian mostró algo que estaba tratando de explicar usando la física y la geometría fractal.

Gray Wood Piet Mondrian, 1911. Museo de arte The La Haya

Mi área de investigación es la biología matemática. Mis colegas y yo estamos tratando de explicar cómo las estructuras de las venas y las arterias, los pulmones y las hojas de threelics, los pulmones y las hojas ajustan con precisión su forma física para administrar sangre, aire, agua y nutrientes de manera efectiva.

La investigación fundamental en ramificación de biología ayuda a ingresar enfermedades cardiovasculares y cáncer, diseñando materiales que pueden curarse y predecir que los árboles responderán al clima variable. El ramificado también aparece en las formas de alimentación de hormigas, moldes deslizantes y ciudades.

Árbol inmobiliario

‘Polder Lander with Siluetirated Young Wood’ por Piet Mondrian, 1900-1901. Wikimedia Commons

Desde 1890. Hasta 1912. Año, Mondrian pintó docenas de árboles. Comenzó con árboles realistas y a todo color en contexto: árboles en granjas o carril moteado. Poco a poco eliminó las hojas, la profundidad, el color y, finalmente, incluso se ramificó de sus pinturas de madera. “Árbol gris” usa solo líneas curvas de diferentes espesores plantados entre sí en esquinas aparentemente accidentales. Aún así, la imagen es un árbol inconfundible.

¿Cómo transmitió Mondrian una sensación de madera con tan poco? La ciencia de los árboles puede ofrecer algunas pistas.

Ciencia de ramificación

Un objetivo de la biología matemática es sintetizar lo que los científicos saben sobre la gran variedad de sistemas de vida, donde existe una excepción a cualquier regla, en principios claros y generales, idealmente con varias excepciones. Uno de esos principios generales es que la evolución está ajustando la estructura de la línea de árboles en los seres vivos para hacer que el metabolismo y la respiración de la manera más eficiente posible.

El cuerpo controla cuidadosamente el grosor del vaso porque las ramas, porque la desviación del diámetro más efectivo consume energía y causa enfermedad, como la aterosclerosis.

En muchos casos, como los vasos sanguíneos humanos, el cuerpo realiza un control mucho más fuerte del diámetro en relación con la longitud. Entonces, si bien las venas y las arterias podrían tomar las rutas circulares para adaptarse a Verila y anatomía, su diámetro generalmente permanece dentro del 10% de óptimo. El mismo principio también aparece en las ramas de los árboles.

La calibración precisa del diámetro de la rama conduce a las características de las formas fractales llamada escala invariante. La escala invariante es una propiedad que tiene una verdad independientemente del tamaño de un objeto o parte del elemento que esté viendo. La escala invariante ocurre en los árboles porque el tronco, las extremidades y las ramitas son todas ramas de manera similar y por razones similares.

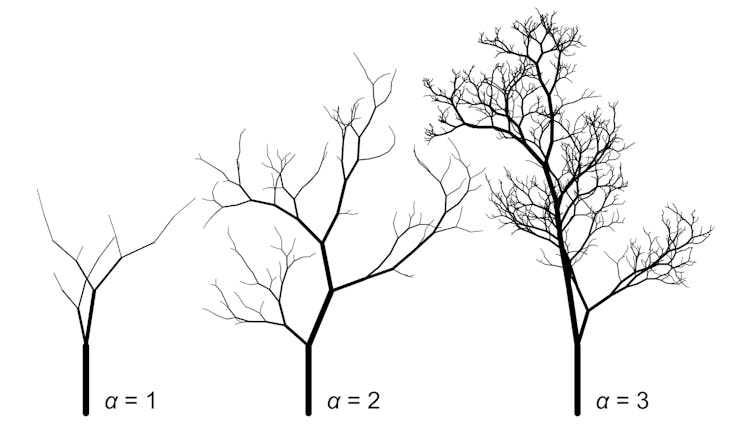
Árboles con diferentes valores de parámetro de escala α. Gao y Newberry / PNAS Nexus

La escala invariante en el diámetro de la rama dicta cuán pequeña debe ser la extremidad como la rama y la cantidad de árbol de inversión en algunas ramas gruesas opuestas a muchas delgadas. Los árboles han desarrollado la escala del invariante para el transporte de agua, alcanzando la luz y resistir la gravedad y la carga del viento, lo cual es posible dar límites físicos de manera más eficiente.

Esta ciencia de los árboles nos inspiró a mi colega y a mí a medir el diámetro de la rama de los árboles en el arte.

El arte de los árboles

Entre mis fotos favoritas se encuentra la talla de madera de la mezquita medieval fallecida en la India. Su surgimiento de árboles me recuerda al gondor de madera de Tolkien y la capacidad humana para apreciar la simple belleza de los seres vivos.

Siddy dijo la mezquita en Ahmedabad, Gujarat, India, c. 1572. Shivrekha / Vikimedia Commons

Pero también encuentro inspiración matemática en la era de oro islámica, el momento en que el arte, la arquitectura, las matemáticas y la física tienen éxito. Los arquitectos islámicos medievales incluso decoraron edificios con patrones infinitamente innecesarios de depósitos que no entendieron las matemáticas occidentales al siglo 20.

‘CvJetachi Blossoms’ de Matsumura Goshuna (1752-1811). Museo Metropolitano de Artes

La mezquita Sidi Saiyed estilizada de leña también sigue el sistema preciso de proporciones dictada por el invariante de árboles reales. Este nivel de diámetro de la rama de precisión requiere cuidadosamente el ojo y el plan cuidadoso, mucho mejor de lo que podría liberar.

De hecho, donde sea que nuestro equipo mirara los árboles en una gran obra artística, como “Lifetime” de Klimtov o “Flowers” de Matsumura Goshun “, también encontramos un invariante preciso en el diámetro de la rama de diámetro.

El “árbol gris” también registra de manera realista las variaciones naturales en los diámetros de la rama, incluso cuando la pintura le da a un espectador un pequeño segundo para continuar. Sin una escala realista, ¿sería esta imagen un árbol?

Al igual que probar el punto, Mondrian ordenó el próximo año, también con un fondo gris, líneas curvas y la misma composición general y dimensiones. Incluso la posición de algunas líneas es la misma.

Pero en “Apple Blossom” (1912), todas las líneas son el mismo grosor. La escala se ha ido, y con él, un árbol. Antes de leer el título, la mayoría de los espectadores no adivinarían que esta era una pintura de árboles. Sin embargo, los bocetos de Mondrian revelan que la “manzana en flor” y la “madera gris” también el mismo árbol.

“CvJeta Jabuka” Piet Mondrian, 1912 Museo de arte de La Haya

Las dos imágenes contienen varios elementos que podrían indicar la madera, una concentración de las líneas cerca del centro, una línea que puede ser ramas o troncos y líneas centrales que pueden indicar país u horizonte.

Sin embargo, solo la “madera gris” tiene diámetros de rama. Cuando Mondrian elimina la invariante en la “manzana floreciente”, los espectadores son fáciles de ver peces, escamas, bailarines, agua o simplemente formas innecesarias, mientras que el árbol en el “árbol gris” es infalible.

Síntesis de fotos

Las imágenes de los árboles de Mondrian y la teoría científica enfatizan la importancia del grosor de los árboles. El examen es cuando diferentes líneas de evidencia y razonamiento llegan a las mismas conclusiones. El arte y las matemáticas exploran las descripciones abstractas del mundo, por lo que se ve un gran arte y ciencia, las mismas características sustanciales de los árboles se cumplen con lo que la habilidad o la ciencia pueden lograr por sí mismas.

Al igual que una gran literatura como “excesivamente” y “deseos de botanika” nos muestran cómo los árboles afectan nuestras vidas en la forma en que no notamos, el arte y la ciencia sobre los árboles muestran que las personas están finamente adaptadas a lo que es importante. Creo que esta resonancia es una de las razones por las que las personas encuentran fractales y paisajes naturales tan agradables y convincentes.

Todas estas líneas de pensamiento nos dan nuevas formas de apreciar los árboles.