El Clásico entre Real Madrid y Barcelona es mucho más que un partido, es un espectáculo deportivo que también permite aplicar herramientas matemáticas para comprender mejor lo que sucede en el terreno de juego. En este artículo exploraremos cómo la métrica de goles esperados (kG) combinada con los diagramas de Venn ofrece una nueva perspectiva sobre el partido más visto del fútbol español.
Los primeros representan métricas modernas aplicadas al fútbol, y los segundos nos conectan con los conceptos clásicos de lógica y teoría de conjuntos, que también reviven nuestros recuerdos escolares.
La combinación de ambos permite actualizar los conceptos desarrollados por el matemático John Wen, cuyo trabajo sigue vigente más de un siglo después de su muerte.
Objetivos potenciales
¿Qué son los kg y qué es el diagrama de Venn?
kG (goles esperados) es una estadística avanzada que se utiliza en el fútbol para medir la “facilidad” de un tiro que resulta en gol, teniendo en cuenta factores como la posición, la situación del portero y la presión defensiva.
Por otro lado, los diagramas de Venn son representaciones gráficas que muestran relaciones entre conjuntos: intersección, unión y complementariedad.
En fútbol tenemos tres resultados posibles que podemos representar en un diagrama de Venn con dos conjuntos y su intersección. Por eso necesitamos tres áreas diferentes para ganar en casa (Barcelona), ganar fuera (Real Madrid) y empatar.
Para ello utilizaremos los eventos B (resultados de Barcelona) y R (resultados de Real Madrid), que serán verdaderos o falsos en función del resultado del partido.
Para representarlos esquemáticamente, necesitamos conjuntos que los representen. Los eventos B y R se convertirán en conjuntos con el mismo nombre. Esta es la secuencia y sus equivalencias generales:
Lenguaje natural → lógica proposicional → teoría de conjuntos:
B o R ⇒ B ∨ R ⇒ B ∪ R
B y R ⇒ B ∧ R ⇒ B ∩ R
Sin B ⇒ ¬B ⇒ Bc
Aplicación a la clásica: conjuntos y probabilidades.
Tomemos como ejemplo el último clásico disputado el 11 de mayo de 2025, que ganó el Barcelona (4-3). Estos son los tiros con mejores valores de kG y sus autores, los que acabaron con el gol coloreado en verde:
Tiros clásicos. Elaborado por el autor.
Ilustraremos este resultado más adelante utilizando la métrica de goles esperados antes del puntapié (kG).
Las cuotas de cada equipo nos dan un valor de probabilidad de gol que va desde 0 (fallar todos) hasta el total de tiros (acertar todos). Los resultados posibles son todas las combinaciones entre los goles de un equipo y el otro, más los fracasos totales. Esto nos da un total de 24 (Barcelona 23 tiros) multiplicados por 10 (Real Madrid 9 tiros), 240 resultados posibles que componen el espacio muestral del experimento. Estos 240 elementos se incluyen en nuestro diagrama de Venn en sus respectivos apartados, según conjuntos:
B (Barcelona, kG 4,27): resultados en los que el Barcelona marca gol, 185 victorias + 10 empates.
R (Real Madrid, kG 2,74): resultados en los que el Real Madrid marca gol, 45 victorias + 10 empates.
B ∩ R: Intersección de priores que representan empates, 10 debido a nueve empates con goles y uno sin goles.
Visualización: diagrama de Venn
Aunque los diagramas de Venn clásicos no representan probabilidades cuantitativamente, en nuestro enfoque visual personalizado, el área de cada círculo se ajusta proporcionalmente a la probabilidad del resultado (ganar, perder, empatar). Esto te permite visualizar no sólo las relaciones lógicas entre eventos, sino también su peso relativo en el contexto del juego. Este nuevo enfoque representa una aplicación directa de los diagramas de Venn en los deportes, específicamente en el fútbol, que se presentó por primera vez en este artículo. Además, plantea dos problemas matemáticos adicionales a resolver:
Problema 1: Con los datos del área (A), calcularemos los radios de cada conjunto.
A = πr2r = √(A / π)
Tarea 2: Con información sobre el área de la sección transversal (A∩), calcularemos la distancia entre los centros (d).
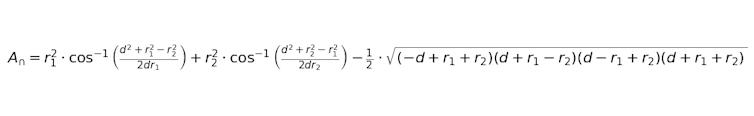
Para asegurarnos de que la sección tenga su área adecuada, necesitamos dibujar los centros de cada círculo a una distancia d, cuyo valor se obtiene resolviendo esta ecuación por métodos numéricos.
En este caso utilizamos el método de Newton-Raphson. Es una de las herramientas más poderosas en matemáticas e ingeniería para resolver ecuaciones no lineales. Este algoritmo numérico se basa en el concepto de derivadas para encontrar raíces de funciones mediante un proceso iterativo. Desarrollado originalmente por Isaac Newton y Joseph Raphson en el siglo XVII, este método ha evolucionado y se ha adaptado a diversas aplicaciones modernas, desde la física hasta la economía.
El diagrama ayuda a visualizar que, aunque el marcador estuvo igualado (4-3), el Barça tuvo más oportunidades de gol de calidad, lo que respalda su victoria desde una perspectiva estadística.
Esta representación nos ofrece los resultados que buscábamos y muestra los méritos de cada equipo de una forma muy visual e intuitiva.
Probabilidades de puntuación final con kG
Probabilidad de victoria del Barcelona: 64,83%.
Probabilidad de empate: 13,34%.
Probabilidad de victoria del Real Madrid: 21,83%.
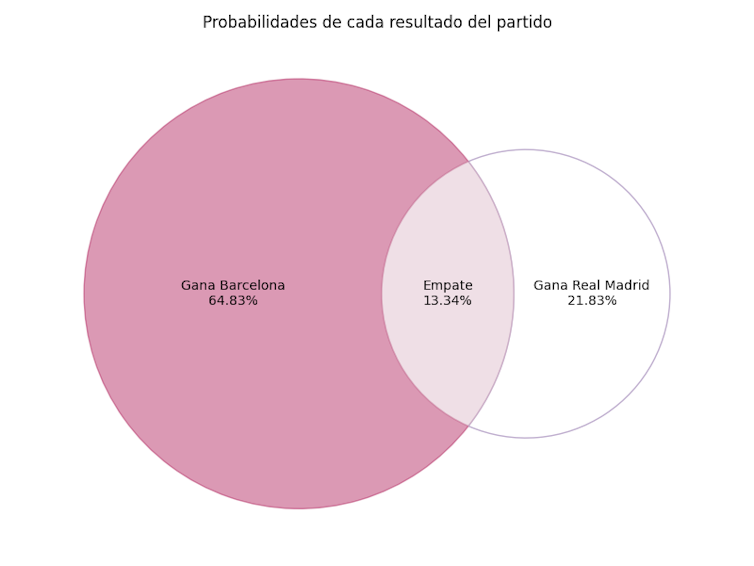
Diagrama de Venn Barcelona – Real Madrid. Elaborado por el autor. Conclusión
Los diagramas de Venn, tradicionalmente asociados con la enseñanza escolar de la lógica y la teoría de conjuntos, encuentran en este artículo una nueva aplicación en el análisis deportivo. Combinarlos con métricas avanzadas como los goles esperados (kG) abre una nueva forma de representar visualmente no sólo las relaciones lógicas entre los posibles resultados de un partido, sino también sus probabilidades relativas que los hacen comparables.
Este enfoque nos permite ir más allá del puntaje final y explorar el “mérito” de cada equipo también desde una perspectiva geométrica. En el clásico entre FC Barcelona y Real Madrid, el uso de diagramas de Venn adaptados al contexto futbolístico revela que aunque el marcador estuvo ajustado (4-3), el Barcelona generó más ocasiones de calidad, lo que se traduce en una mayor superficie de su equipo en el diagrama.
En definitiva, este artículo no sólo ofrece una nueva forma de entender los partidos de fútbol, sino que también muestra cómo conceptos matemáticos aparentemente alejados del deporte pueden enriquecer su análisis. Es una invitación a mirar el fútbol con otros ojos: los ojos de la lógica, la probabilidad y la geometría.
Descubre más desde USA Today
Suscríbete y recibe las últimas entradas en tu correo electrónico.









