Las fiestas traen consigo celebración, descanso y, para muchas familias, largos períodos de tiempo en el interior. Para algunos, esto significa que los juegos de mesa están reapareciendo rápidamente en las mesas de la cocina. Los juegos brindan oportunidades para el aprendizaje activo de las matemáticas.
Estos momentos de aprendizaje basados en el juego plantean una pregunta más amplia: ¿Cómo podemos apoyar el aprendizaje de matemáticas de los estudiantes en casa sin convertir el recreo en lecciones formales?
Una respuesta proviene de una herramienta de aprendizaje en el aula simple pero sorprendentemente poderosa: los rompecabezas de Tarsia. Se trata de rompecabezas creados con el software gratuito Tarsia, de Hermitech Laboratori. El software permite a las personas crear, imprimir y guardar rompecabezas personalizados, actividades de dominó y diversas actividades de clasificación de tarjetas rectangulares.
Para el aula de matemáticas, una hoja de rompecabezas de Tarsia completa impresa en papel generalmente se lamina (para uso múltiple) antes de cortarla en pedazos.
Aprendizaje social y activo que valora los errores
El matemático canadiense Anthony Bonato aconseja: “No importa qué método se utilice para enseñar matemáticas, hazlo divertido. La mayoría de los estudiantes estarían de acuerdo: a menudo falta la alegría en su experiencia”.
Como investigador en educación matemática, añadiría que, independientemente del método utilizado para enseñar matemáticas, el aprendizaje debe ser activo y social, y valorar los errores como oportunidades de aprendizaje. Éstas son las condiciones bajo las cuales los estudiantes se sienten seguros para intentarlo, fallar y volver a intentarlo.
Los rompecabezas de Tarsia, que existen desde hace más de una década y se han utilizado en las aulas K-12, logran todo esto casi sin explicación para los estudiantes. Sin embargo, su uso en las aulas universitarias de matemáticas parece ser poco común.
Mi investigación se centró en por qué el uso de rompecabezas de Tarsia funciona para la enseñanza de matemáticas y su impacto en el aula de pregrado.
Azulejos geométricos a juego
El software Tarsia permite a los profesores incorporar relaciones matemáticas (fracciones, funciones, gráficos, expresiones algebraicas) en mosaicos geométricos como triángulos, rectángulos o rombos.
Los estudiantes deben unir las fichas para que los bordes se alineen y eventualmente formen una forma completa.
El software Tarsia ofrece a los usuarios una variedad de acertijos para elegir.
Hay diferentes tipos de rompecabezas de Tarsia disponibles en el software. (Francisco Dua)
Los maestros de primaria y secundaria utilizan los rompecabezas de Tarsia para fortalecer el sentido numérico y profundizar la comprensión de funciones, gráficas y relaciones algebraicas. Los profesores universitarios pueden utilizarlos para dar vida a temas como los límites, las derivaciones y la integración, áreas donde los estudiantes a menudo se sienten intimidados.
‘datos’ matemáticos
Cada mosaico contiene “datos” matemáticos; por ejemplo, un rompecabezas de Tarsia adecuado para estudiantes de primaria podría incluir piezas marcadas con fracciones, decimales y porcentajes, para ayudar a los estudiantes a comprender equivalentes como ¼ = 25 por ciento.
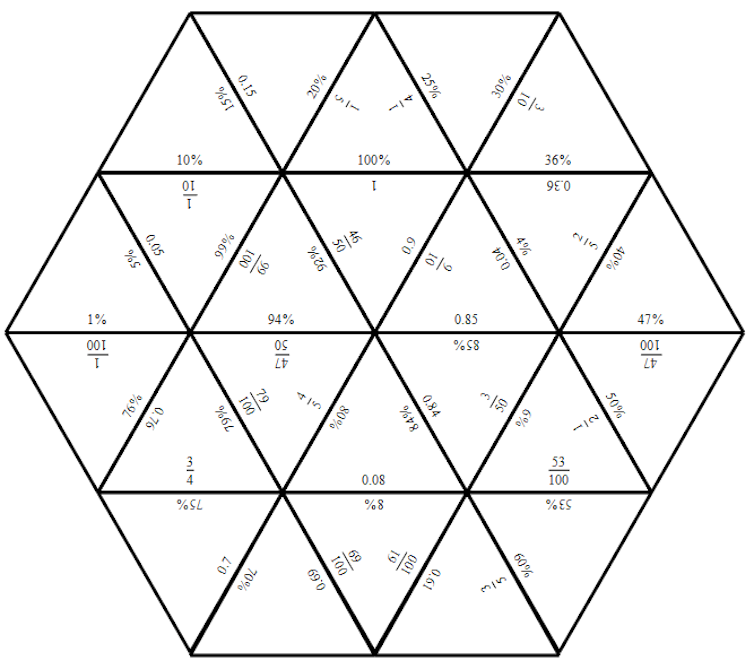
Un rompecabezas completo sobre fracciones, decimales y porcentajes que podría ser adecuado para estudiantes de primaria. (Francisco Dua)
Para un aprendizaje más avanzado, las piezas del rompecabezas pueden mostrar dos fracciones equivalentes, una expresión logarítmica y su forma simplificada, o una función combinada con su gráfica.
En ambos casos, los estudiantes arman el rompecabezas identificando qué piezas van juntas. Cuando todas las fichas coinciden correctamente, aparece una forma completa.
Debido a que los acertijos de Tarsia enfatizan el reconocimiento y las relaciones en lugar de cálculos largos, los estudiantes piensan en cómo se conectan las ideas. Comparan expresiones, notan características gráficas y razonan sobre equivalencias. En muchos sentidos, la actividad imita el pensamiento matemático auténtico.
Los acertijos de Tarsia requieren poca supervisión y la mayor parte del aprendizaje del estudiante ocurre en conversaciones alrededor de la mesa, no en soluciones escritas.
Los estudiantes de matemáticas en los grados 11 y 12 pueden usar un acertijo de Tarsia sobre logaritmos, parte del aprendizaje sobre exponentes o “la potencia a la que se debe elevar la base para obtener un número determinado”.
Por qué es importante el aprendizaje activo
Décadas de investigación han demostrado que los estudiantes aprenden mejor matemáticas cuando discuten problemas, prueban ideas y cometen errores en condiciones de baja presión. Los estudios confirman que el aprendizaje activo mejora la comprensión, reduce las tasas de fracaso y genera confianza entre las materias STEM.
Sin embargo, muchas aulas de matemáticas todavía funcionan como conferencias unidireccionales, donde los estudiantes copian procedimientos en silencio y esperan seguirlos.
Los rompecabezas de Tarsia invierten este patrón. Crean una resolución de problemas estructurada y colaborativa que se parece más a un juego que a una evaluación. Un estudiante que teme las demostraciones formales aún puede desear conectar la derivada con su gráfica. Alguien a quien no le gustan las fracciones puede sentir menos presión cuando una suposición incorrecta simplemente significa probar con otra ficha.
Un rompecabezas desafiante podría combinar piezas cuadradas y triangulares en una figura de 10 lados, lo que ayudaría a enseñar límites, secuencias, series y derivadas parciales en cálculo multivariable.
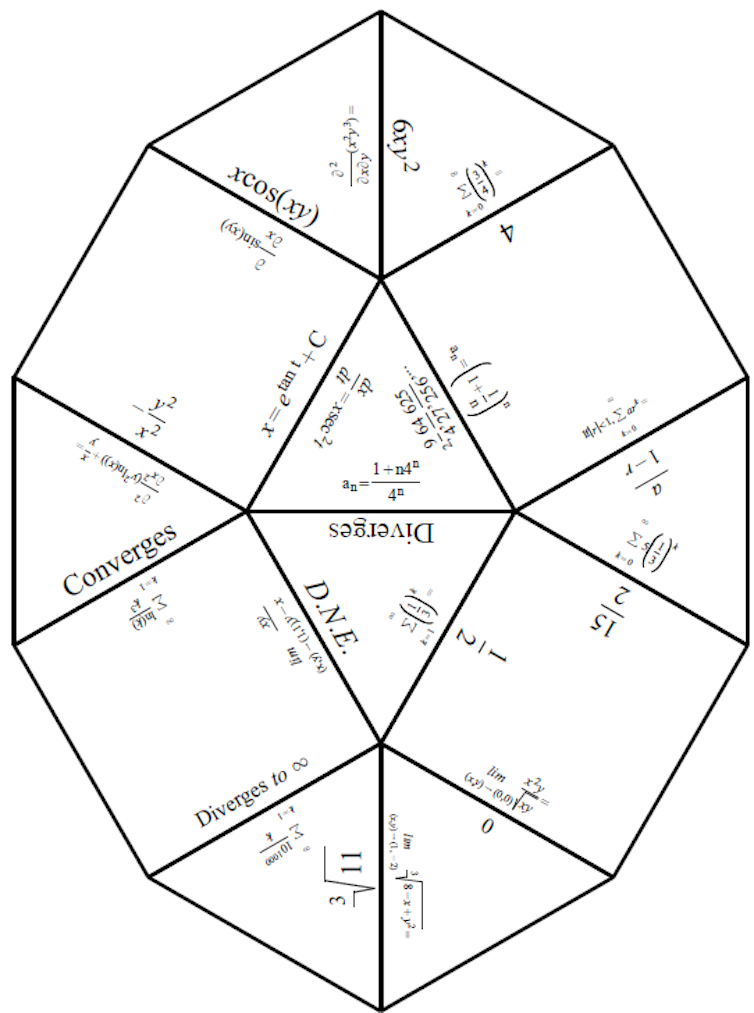
Rompecabezas completado sobre límites, secuencias, series y derivadas parciales. (Francis Dua) Un estudio reciente
En el aula de aprendizaje activo de la Universidad Metropolitana de Toronto, mis colegas y yo exploramos cómo los rompecabezas de Tarsia ayudan a los estudiantes de primer año a aprender cálculo, aprovechando la reflexión estructurada y la retroalimentación de los estudiantes para examinar nuestras propias prácticas de enseñanza.
Varios temas surgieron consistentemente del análisis de nuestras notas reflexivas sobre los estudiantes que usaron Tarsia Puzzles:
Menos miedo: Los estudiantes que normalmente estaban preocupados por cometer errores participaron más libremente. Los errores se convirtieron en parte del proceso de resolución de acertijos en lugar de defectos personales.
Más conversación: los estudiantes discutieron ideas, explicaron razonamientos y se corrigieron unos a otros, comportamientos que rara vez se ven en las tutorías tradicionales.
Mejor participación: los estudiantes trabajaron más tiempo y con mayor concentración en comparación con las tareas basadas en hojas de trabajo. Algunos que normalmente empacaban temprano se quedaron para completar el rompecabezas.
Por qué los padres y educadores deberían preocuparse
Las matemáticas a menudo se presentan como un trabajo solitario, pero los matemáticos colaboran constantemente: discuten, verifican, revisan y proponen alternativas. Los estudiantes se benefician de interacciones similares.
En casa o en pequeños grupos de tutoría, el rompecabezas Tarsia ofrece una entrada de bajo riesgo al razonamiento matemático. Los estudiantes que se muestran reacios a hablar en clase pueden identificar con seguridad aristas no coincidentes o preguntarse si dos expresiones son equivalentes. Los conceptos erróneos se revelan naturalmente a través del rompecabezas, lo que permite una corrección suave y sin vergüenza.
Para probar los acertijos de Tarsia, los padres y educadores de estudiantes jóvenes podrían probar ejemplos adecuados para estudiantes de primaria y secundaria superiores.
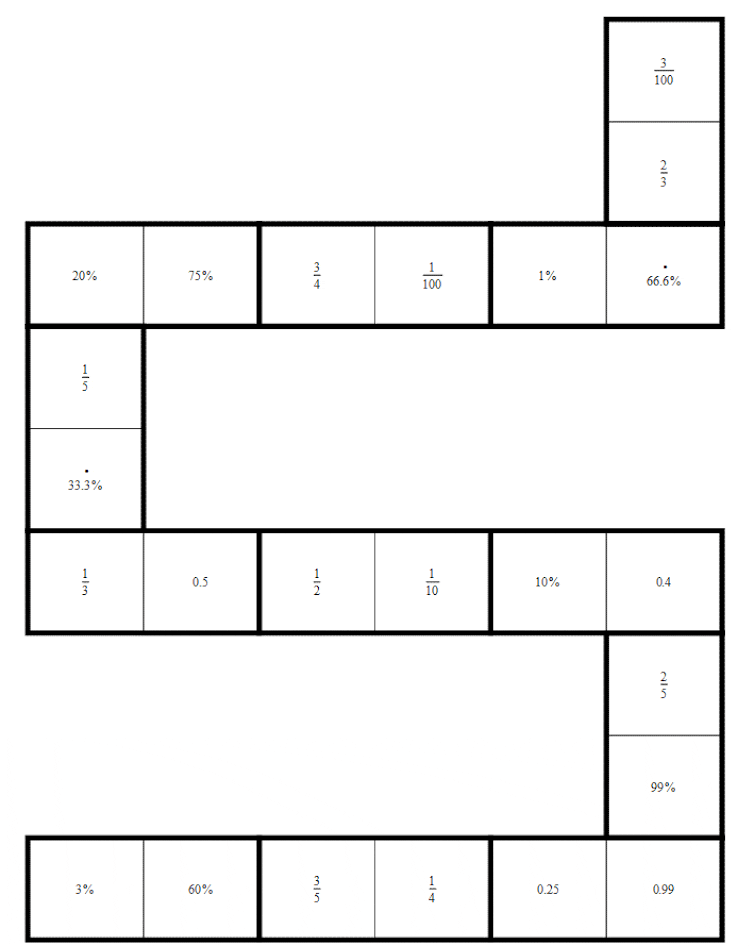
Un rompecabezas estilo dominó sobre fracciones, decimales y porcentajes. (Francisco Dua)
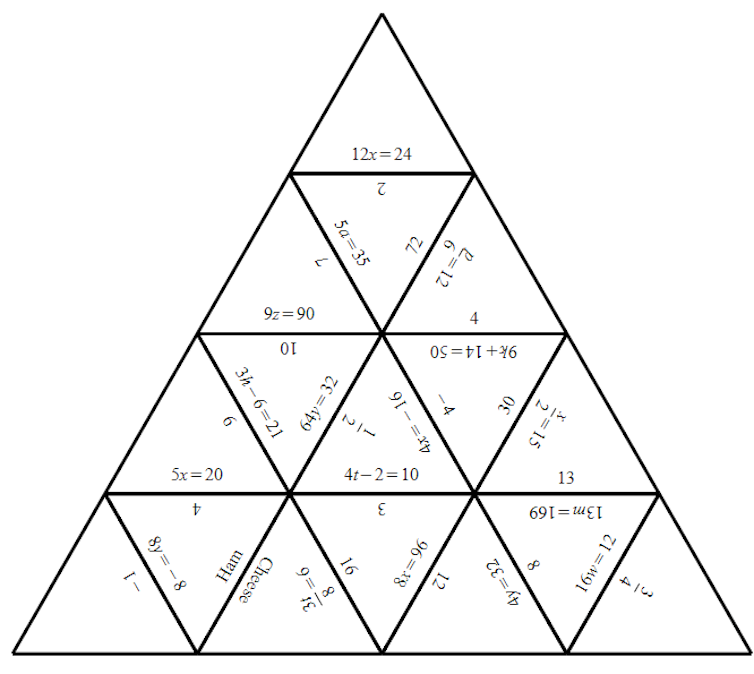
Un acertijo sobre ecuaciones lineales. (Francis Dua) Convocatoria de desarrolladores
El software Tarsia es útil pero está desactualizado. Actualmente se ejecuta en el sistema operativo Windows.
Una versión moderna basada en la web, con herramientas de colaboración, plantillas alineadas con el plan de estudios y accesibilidad integrada, ampliaría enormemente su adopción. Los desarrolladores de tecnología educativa que busquen herramientas eficaces y de bajo coste podrían encontrar aquí un enorme potencial.
Las matemáticas se vuelven más fáciles cuando despiertan la curiosidad. Los rompecabezas de Tarsia, de diseño modesto pero de efecto poderoso, alientan a los estudiantes a hablar, pensar y tomar riesgos intelectuales. Ayudan a padres, profesores e instructores a ver el razonamiento de los estudiantes en tiempo real, no sólo sus respuestas finales.
Lo más importante es que traen de vuelta una verdad a menudo olvidada: las matemáticas pueden ser divertidas y el aprendizaje se produce a través de la conversación.
Descubre más desde USA Today
Suscríbete y recibe las últimas entradas en tu correo electrónico.









